[켈리공식 A to Z] 1-5. 켈리공식을 본격 수식적으로 나타내보기

해당 글은 시리즈로 연재되고 있으며

이전 글을 안 읽으셨다면 이전의 글부터 먼저 읽어보길 추천드립니다.

우선 켈리공식 A to Z 시리즈를 시작하기에 앞서...

 

본격적으로 수식이 나오는 구간이니 여기서부턴 집중을 더 해주셔야 합니다.

그 전에 이 영상을 보고 나시면 아래 내용이 더 이해가 잘 되실겁니다.

https://youtu.be/C3Sdc_7e5Og?si=MQsw_dnLJMCoUr9d

 

예전에 예시를 든 확률 반반으로(50%:50%) 베팅금액의 이겼을 때 60%를 졌을 때 -40%가 되는 게임 다시 한번 생각해보겠습니다.

자금을 베팅하는 비율에 따라 게임이 진행되는 것을 수식으로 표현해야 한다면?

이 게임을 수학적으로는 어떻게 표현해야 할까요?

 

이렇게 한번 표시해보겠습니다.

n = n회차 게임을 한다고 할 때 게임 횟수

f = 베팅 비율 (아무것도 베팅하지 않으면 0 내 전체 자금을 베팅하면 1(100%) 절반만 베팅하면 0.5(50%)

w(n) = n회차 게임을 할 때 이긴 횟수

L(n) = n회차  게임을 할 때 진 횟수

S(n) = n회차 게임을 했을 때 자금이 불어난 비율(초기값은 1이라고 생각한다면...)

 

n회차 게임을 한다고 했을 때 초기자금에 비해서 얼마나 자금이 불어났는지 S(n)을 한번 나타내 보겠습니다. (그림판으로...)

여기서 우리는 앞 시간에 f가 42%만큼 베팅하는 것이 합리적이다 라고 알고 있지만 우선 f에 1(100%)을 대입해보겠습니다.(계산하기 쉽게 하기 위해서)

또 이긴 횟수와 진 횟수의 총합은 전체 게임을 한 횟수인 n번이 되어야겠죠? 즉 W(n)과 L(n)을 합하면 n이 되어야 합니다. 여기서 10번을 게임했다고 가정해보겠습니다. 확률은 반반이긴 하지만 게임을 해보니 7번 이기고 3번 졌다고 해보겠습니다. 이 경우의 S(10)은 어떻게 될까요?

이 경우의 S(10)은 다 대입해보면

 

S(10) = ( 1 + 0.6 ) ^ 7 × ( 1 - 0.4 ) ^ 3 = 5.7982058496(579.820...%)

 

원금이 1이라고 했을 때에 풀베팅(100%)을 한다면 이긴 횟수가 7 진 횟수가 3이면 원금이 579%로 불어나게 됩니다.

 

 

S(n)의 경우 정의가 n회차 게임을 했을 때 자금이 불어난 비율이라고 설명드렸었죠?

그렇다면 n번게임을 했을 시 1 회차당 게임을 했을 때 자금이 불어난 비율은 어떻게 표시를 하는 게 좋을까요?

정답은

이것이 이해가 되지 않는다면 기하평균에 대한 이해를 아직까지 못하고 있는 겁니다.

 

왜 1/n승을 해야하는지 이해가 안된다면 같이 읽으면 좋은 글(링크)

기하평균을 쓰는 이유

 

(S(n))^(1/n)의 그렇다면 우측 항은 어떻게 될까요?

이렇게 되겠죠.

 

위의 예시에서 겨우 10번만 게임을 했을 때 W(n)이 7번 L(n)이 3번 나오는 경우의 예시를 들었습니다.

그런데 말입니다. 

이게임을 10번 말고 1000번... 10000번...... 아니 무한대로 게임을 해보면 어떻게 될까요??

수많은 게임을 한다면???

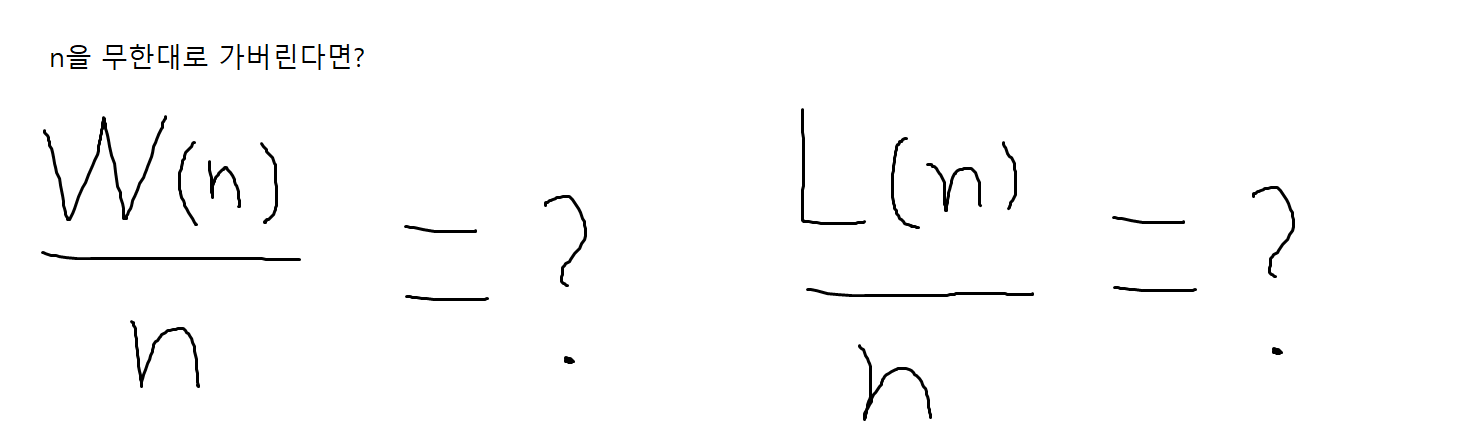
이럴 때는 이 두 개의 값은 얼마가 될까요?

사실 우리는 정답을 이미 알고 있습니다. 그 이유는? 애초에 이길 확률과 질 확률은 이미 가정했으니까요.

게임을 하면 할수록 각각 이길 확률과 질 확률이 수렴하게 될 것입니다. 이긴 횟수를 시행 횟수로 나누어보고 진 횟수를 시행 횟수로 나누었을 때 무한 번 반복한다면? 결국 확률에 수렴하게 됩니다.

 

즉

W(n)/n 도 n의 횟수를 늘릴수록 0.5(50%)

L(n)/n 도 n의 횟수를 늘릴수록 0.5(50%)

로 수렴을 하게 됩니다.

 

겨우 10번 정도의 시행에서 는 이길 횟수가 7번 질 횟수가 3번 정도인 것은 이해가 가지만(물론 10번 다 이길 수도 있고 아닐 수도 있지만...) 수천... 수만 번... 무한대로 시행했을 때는 거의 시행 횟수의 각각 절반에 수렴할 것입니다.

 

즉, n번게임을 했을 시 1 회차당 게임을 했을 때 자금이 불어난 비율을 lim(n->∞) 시행 횟수를 무한으로 보내버림으로써 평균 1 회차당 게임을 했을 때 자금이 불어난 비율로 바뀌게 되는 것입니다.

 

따라서 lim(n->∞)(S(n)^(1/n))의 경우는 평균 1번 게임당 자금이 늘어나는 것이 영향을 받는 변수는 f밖에 없기 때문에

g(f)라고 가정하겠습니다.

 

 

이때 미분을 해서 0이 나오는 값이 최댓값이 나오는 지점이며 우리는 0.42(42%) 정도를 투자했을 때 그 값이 최댓값이 되는 것을 이미 알고 있습니다.

g(f)에 0.42를 대입한다면? 1.02061941976429196298481255691....(102.061941..%)라는 값이 나오게 되는데

 

이는 평균 게임을 할 때마다 약 2% 정도씩 복리수익을 기대할 수 있다는 의미입니다.

다음은 이겼을 때 졌을 때 바로 나뉘는 단일 경우 말고 4가지 case로 나누고 다시 한번 g(f)를 구해보는 시간을 가져보겠습니다.

 

다음 글

1-5. 켈리공식을 본격 수식적으로 나타내보기(추가설명)