[켈리공식 A to Z] 번외편. Proebsting's paradox

https://en.wikipedia.org/wiki/Proebsting%27s_paradox

Proebsting's paradox - Wikipedia

그냥 여기에 있는 나무위키 번역하는 것 + 제 개인적인 생각을 설명 덧붙여서 진행하도록 하겠습니다. 개인적 생각 부분은 다른 색깔로 표시하겠습니다.

 

In probability theory, Proebsting's paradox is an argument that appears to show that the Kelly criterion can lead to ruin. Although it can be resolved mathematically, it raises some interesting issues about the practical application of Kelly, especially in investing. It was named and first discussed by Edward O. Thorp in 2008.[1] The paradox was named for Todd Proebsting, its creator.

 

이 확률 이론에서 프로브스팅의 역설(Proebsting's paradox)은 켈리 기준이 파산으로 이어질 수 있다는 주장을 나타내는 역설입니다. 이 문제는 수학적으로 해결될 수 있지만, 특히 투자에서 켈리 기준의 실제 적용에 관한 흥미로운 이슈를 제기합니다. 이 역설은 2008년 에드워드 O. 소프(Edward O. Thorp)에 의해 처음 논의되고 명명되었으며, 그 창시자는 토드 프로브스팅(Todd Proebsting)입니다.

 

역설의 정의

 

If a bet is equally likely to win or lose, and pays b times the stake for a win, the Kelly bet is:

확률이 동일하게 승리하거나 패할 가능성이 있는 내기에서 승리 시 배당이 베팅 금액의 b배라면, 켈리 기준에 따른 최적 베팅 비율은 다음과 같습니다:

times wealth. For example, if a 50/50 bet pays 2 to 1, Kelly says to bet 25% of wealth. If a 50/50 bet pays 5 to 1, Kelly says to bet 40% of wealth.

 

즉, 전체 재산의 이만큼을 베팅해야 합니다. 예를 들어, 50/50 확률의 내기가 2 대 1 배당을 제공할 경우, 켈리 기준은 재산의 25%를 베팅하라고 합니다. 50/50 내기가 5 대 1 배당을 제공할 경우에는 재산의 40%를 베팅하라고 합니다.

 

Now suppose a gambler is offered 2 to 1 payout and bets 25%. What should he do if the payout on new bets changes to 5 to 1? He should choose f* to maximize: 

 

이제 도박사가 2 대 1 배당을 제시받고 25%를 베팅했다고 가정해 보겠습니다. 새로운 배당이 5 대 1로 바뀌면 어떻게 해야 할까요? 그는 다음 식을 최대화하도록 f*  선택해야 합니다:

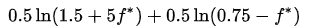
because if he wins he will have 1.5 (the 0.5 from winning the 25% bet at 2 to 1 odds) plus 5f*; and if he loses he must pay 0.25 from the first bet, and f* from the second. Taking the derivative with respect to f* and setting it to zero gives:

 

추가설명 : 이 식이 이해가 안가신다면 켈리공식 시리즈를 처음부터 보세요.

0.5(이길확률 : 빈도50%) * log(1.5(25%를 베팅했을 때 이겼을 때 결과값) + 5f (새로운 내기의 이겼을 때 배당의비율) ) + 0.5(질확률 : 빈도 50%) *log(0.75(25%를 베팅했을 때 졌을 때 결과값) -f(새로운 내기의 졌을 때 배당비율))

이걸 최대화하려면? 미분값이 0이어야 되겠죠?

 

이는 그가 승리할 경우, 1.5 (2 대 1 배당에서 25% 베팅으로 얻은 0.5)와 5 f* 를 가지게 되며, 패할 경우 첫 번째 베팅에서 0.25, 두 번째 베팅에서 f* 를 지불해야 하기 때문입니다. 이를 f* 에 대해 미분하고 0으로 설정하면 다음과 같은 방정식을 얻습니다:

추가설명 : 미분과정은 다음과 같습니다.

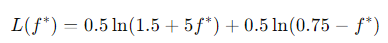
f*이 최대화가 되는 곳이 f*'= 0이 되는 곳이기 때문에

 

첫번째 항의 미분

두번째 항의 미분

그것들의 합의 미분 값

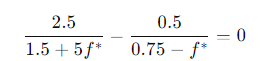
의 결과로 위와 같은 결론이 나옴.

 

 

which can be rewritten:

이를 정리하면

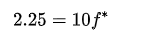
So f* = 0.225.

따라서 f∗=0.225입니다.

 

The paradox is that the total bet, 0.25 + 0.225 = 0.475, is larger than the 0.4 Kelly bet if the 5 to 1 odds are offered from the beginning. It is counterintuitive that you bet more when some of the bet is at unfavorable odds. Todd Proebsting emailed Ed Thorp asking about this.

 

여기서 역설은 전체 베팅 금액이 0.25 + 0.225 = 0.475로, 처음부터 5 대 1 배당을 제시받았을 때의 0.4보다 크다는 점입니다. 불리한 배당 조건에서도 더 많은 금액을 베팅하게 되는 것이 직관에 어긋납니다. 토드 프로브스팅은 이 문제를 에드 소프에게 이메일로 문의했습니다.

 

추가설명 :

첫번째 베팅

 - 배당률 : 2 대 1

 - 켈리기준 베팅 : 25%

두번째 베팅

 - 배당률 : 5 대 1

 - 켈리기준 베팅비율 : 재산의 22.5%

 

총 베팅금액 : 0.25 + 0.225 = 0.475(재산의 47.5%)

처음 5대 1 배당을 제시 받았을 때 켈리기준 베팅금액은 재산의 40%인데 반해. 불리한 배당조건(2 대 1)에서 베팅했음에도 '전체 베팅 금액이 더 커졌습니다. 직관적으로는 배당률이 좋아지면, 더 좋은 조건에서 더 많은 금액을 베팅하고 싶고, 불리한 조건에서는 베팅금액을 줄이거나 아예 베팅을 하지 않는 것이 합리적인데, 불리한 조건에서 이미 베팅한 금액이 있는데 좋은 조건에서도 추가로 베팅해서, 총 베팅금액이 처음부터 좋은 조건에서만 베팅했을 떄 보다 더 많아진 것입니다.

 

불리한 조건에서 시행한 베팅이 전체 베팅 금액을 '더 늘리는' 상황인 것입니다.

 

 

Ed Thorp realized the idea could be extended to give the Kelly bettor a nonzero probability of being ruined. He showed that if a gambler is offered 2 to 1 odds, then 4 to 1, then 8 to 1 and so on (2n to 1 for n = 1 to infinity) Kelly says to bet:

each time.

 

에드 소프는 이 아이디어가 켈리 베터가 파산할 확률이 0이 아닌 상황으로 확장될 수 있음을 깨달았습니다. 예를 들어, 도박사가 2 대 1 배당, 그다음 4 대 1, 이후 8 대 1 등 (n이 1에서 무한대까지 갈 때 2n 대 1 배당)을 제시받을 경우, 켈리 기준은 매번 다음과 같이

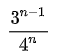
베팅하라고 합니다:

 

The sum of all these bets is 1. So a Kelly gambler has a 50% chance of losing his entire wealth.

In general, if a bettor makes the Kelly bet on a 50/50 proposition with a payout of b1, and then is offered b2, he will bet a total of:

 

이 모든 베팅의 합은 1이 됩니다. 따라서 켈리 베팅자는 재산을 전부 잃을 확률이 50%입니다.

일반적으로, 배터가 50/50 확률의 첫 번째 베팅에서 b1b_1b1​ 배당을 받았고, 이후 b2b_2b2​ 배당을 제시받았다면, 그는 다음과 같이 총 베팅합니다:

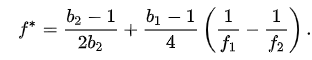
The first term is what the bettor would bet if offered b2 initially. The second term is positive if f2 > f1, meaning that if the payout improves, the Kelly bettor will bet more than he would if just offered the second payout, while if the payout gets worse he will bet less than he would if offered only the second payout.

 

첫 번째 항은 처음부터 b2를 제시받았을 때의 베팅 금액을 나타냅니다. 두 번째 항은 f2>f1일 때 양수가 되어, 배당이 개선되면 켈리 베터는 두 번째 배당만 제시받은 경우보다 더 많은 금액을 베팅하며, 배당이 나빠지면 그 반대로 베팅합니다.

 

응용

 

Many bets have the feature that payoffs and probabilities can change before the outcome is determined. In sports betting for example, the line may change several times before the event is held, and news may come out (such as an injury or weather forecast) that changes the probability of an outcome. In investing, a stock originally bought at $20 per share might be available now at $10 or $30 or any other price. Some sports bettors try to make income from anticipating line changes rather than predicting event outcomes. Some traders concentrate on possible short-term price movements of a security rather than its long-term fundamental prospects.

 

많은 내기는 결과가 결정되기 전에 배당금과 확률이 변할 수 있는 특징을 가지고 있습니다. 예를 들어, 스포츠 베팅에서는 이벤트가 열리기 전에 여러 차례 배당률이 바뀔 수 있으며, 부상이나 날씨 예보와 같은 뉴스가 결과의 확률을 바꿀 수 있습니다. 투자에서도 처음 주식을 1주당 20달러에 샀다가 지금은 10달러, 30달러 또는 다른 가격으로 거래될 수 있습니다. 일부 스포츠 베터들은 경기 결과를 예측하는 대신 배당률의 변화를 예상해 수익을 내려고 합니다. 일부 트레이더들은 증권의 장기적인 근본적 전망보다 단기적인 가격 변동에 집중하기도 합니다

 

A classic investing example is a trader who has exposure limits, say he is not allowed to have more than $1 million at risk in any one stock. That doesn't mean he cannot lose more than $1 million. If he buys $1 million of the stock at $20 and it goes to $10, he can buy another $500,000. If it then goes to $5, he can buy another $500,000. If it goes to zero, he can lose an infinite amount of money, despite never having more than $1 million at risk.

 

고전적인 투자 예로는 노출 한도가 있는 트레이더를 들 수 있습니다. 예를 들어, 특정 주식에 100만 달러 이상 위험을 감수할 수 없다는 규정이 있다고 해봅시다. 이는 그가 100만 달러 이상을 잃을 수 없다는 뜻이 아닙니다. 그가 주식을 20달러에 100만 달러어치 매수했는데 주가가 10달러로 떨어지면 50만 달러를 추가로 매수할 수 있습니다. 주가가 5달러로 떨어지면 또다시 50만 달러를 매수할 수 있습니다. 주가가 0이 되면, 그는 한 번도 100만 달러 이상을 투자하지 않았음에도 불구하고 무한한 금액을 잃을 수 있습니다.

 

해결방안

 

There is no paradox. Kelly's criterion is to maximise expected rate of growth; only under restricted conditions does it correspond to maximising the log. One easy way to dismiss the paradox is to note that Kelly assumes that probabilities do not change.

 

역설은 존재하지 않습니다. 켈리 기준은 기대 성장률을 최대화하기 위한 것이며, 제한된 조건에서만 로그를 최대화하는 것과 일치합니다. 이 역설을 쉽게 무시할 수 있는 방법 중 하나는 켈리가 확률이 변하지 않는다고 가정한다는 점을 지적하는 것입니다.

 

A Kelly bettor who knows odds might change could factor this into a more complex Kelly bet. For example suppose a Kelly bettor is given a one-time opportunity to bet a 50/50 proposition at odds of 2 to 1. He knows there is a 50% chance that a second one-time opportunity will be offered at 5 to 1. Now he should maximize:

 

배당률이 변할 수 있다는 것을 아는 켈리 베팅자는 이를 더 복잡한 켈리 베팅에 반영할 수 있습니다. 예를 들어, 켈리 베팅자가 50/50 내기에 2 대 1 배당으로 한 번의 기회를 제공받았다고 가정해 보겠습니다. 그는 50% 확률로 5 대 1 배당의 또 다른 한 번의 기회를 제공받을 수 있다는 것을 알고 있습니다. 이 경우, 그는 다음을 최대화해야 합니다:

 

with respect to both f1 and f2. The answer turns out to be bet zero at 2 to 1, and wait for the chance of betting at 5 to 1, in which case you bet 40% of wealth. If the probability of being offered 5 to 1 odds is less than 50%, some amount between zero and 25% will be bet at 2 to 1. If the probability of being offered 5 to 1 odds is more than 50%, the Kelly bettor will actually make a negative bet at 2 to 1 odds (that is, bet on the 50/50 outcome with payout of 1/2 if he wins and paying 1 if he loses). In either case, his bet at 5 to 1 odds, if the opportunity is offered, is 40% minus 0.7 times his 2 to 1 bet.

 

이는 f1 과 f2 모두에 대한 것입니다. 해답은 2 대 1에서 베팅을 하지 않고, 5 대 1에서의 베팅 기회를 기다리며, 그 경우에는 재산의 40%를 베팅하는 것입니다. 5 대 1 배당이 제공될 확률이 50% 미만이라면, 2 대 1에서 0에서 25% 사이의 금액을 베팅하게 됩니다. 만약 5 대 1 배당이 제공될 확률이 50%를 초과하면, 켈리 베팅자는 2 대 1 배당에서 실제로 음수 베팅(즉, 승리 시 1/2, 패배 시 1을 지불하는 50/50 내기에 베팅)을 하게 됩니다. 두 경우 모두 5 대 1 배당에서 제공된 경우의 베팅은 40%에서 2 대 1 베팅의 0.7배를 뺀 값입니다.

 

What the paradox says, essentially, is that if a Kelly bettor has incorrect beliefs about what future bets may be offered, he can make suboptimal choices, and even go broke. The Kelly criterion is supposed to do better than any essentially different strategy in the long run and have zero chance of ruin, as long as the bettor knows the probabilities and payouts.

 

이 역설은 본질적으로 켈리 베팅자가 미래에 제공될 베팅에 대한 잘못된 신념을 가질 경우 최적의 선택을 하지 못하고 심지어 파산할 수도 있다는 점을 시사합니다. 켈리 기준은 베팅자가 확률과 배당을 알고 있는 한, 장기적으로는 본질적으로 다른 어떤 전략보다도 나아야 하며, 파산 가능성은 0이 되어야 합니다

 

More light on the issues was shed by an independent consideration of the problem by Aaron Brown, also communicated to Ed Thorp by email. In this formulation, the assumption is the bettor first sells back the initial bet, then makes a new bet at the second payout. In this case his total bet is:

 

아론 브라운이 독립적으로 이 문제를 고려하면서, 에드 소프와 이메일로 논의한 것이 이 문제에 대한 이해를 높였습니다. 이 해석에서는 베팅자가 처음에는 초기 베팅을 매도한 후, 두 번째 배당에서 새로운 베팅을 하는 것으로 가정합니다. 이 경우, 그의 총 베팅은 다음과 같습니다:

which looks very similar to the formula above for the Proebsting formulation, except that the sign is reversed on the second term and it is multiplied by an additional term.

 

이것은 프로브스팅의 공식과 매우 유사하지만, 두 번째 항의 부호가 반대이며 추가 항에 의해 곱해지는 차이점이 있습니다.

 

For example, given the original example of a 2 to 1 payout followed by a 5 to 1 payout, in this formulation the bettor first bets 25% of wealth at 2 to 1. When the 5 to 1 payout is offered, the bettor can sell back the original bet for a loss of 0.125. His 2 to 1 bet pays 0.5 if he wins and costs 0.25 if he loses. At the new 5 to 1 payout, he could get a bet that pays 0.625 if he wins and costs 0.125 if he loses, this is 0.125 better than his original bet in both states. Therefore his original bet now has a value of -0.125. Given his new wealth level of 0.875, his 40% bet (the Kelly amount for the 5 to 1 payout) is 0.35.

 

예를 들어, 2 대 1 배당 후 5 대 1 배당이 주어진 원래 예를 보면, 이 해석에서는 베팅자가 처음에 2 대 1에서 재산의 25%를 베팅합니다. 5 대 1 배당이 제시되면, 베팅자는 초기 베팅을 0.125의 손실로 매도할 수 있습니다. 그의 2 대 1 베팅은 승리 시 0.5를 지급하고, 패배 시 0.25의 비용이 듭니다. 새로운 5 대 1 배당에서 그는 승리 시 0.625를 지급받고, 패배 시 0.125의 비용이 드는 베팅을 할 수 있습니다. 이는 원래 베팅보다 두 상태에서 모두 0.125 더 나은 조건입니다. 따라서 그의 원래 베팅의 가치는 이제 -0.125입니다. 새로운 재산 수준인 0.875에서의 40% 베팅(5 대 1 배당에서의 켈리 금액)은 0.35입니다.

 

The two formulations are equivalent. In the original formulation, the bettor has 0.25 bet at 2 to 1 and 0.225 bet at 5 to 1. If he wins, he gets 2.625 and if he loses he has 0.525. In the second formulation, the bettor has 0.875 and 0.35 bet at 5 to 1. If he wins, he gets 2.625 and if he loses he has 0.525.

 

두 가지 해석은 동일합니다. 원래 해석에서는 베팅자가 2 대 1에서 0.25를, 5 대 1에서 0.225를 베팅합니다. 그가 승리하면 2.625를 얻고, 패배하면 0.525가 됩니다. 두 번째 해석에서는 베팅자가 0.875를 가지고 5 대 1에서 0.35를 베팅합니다. 승리하면 2.625, 패배하면 0.525가 됩니다.

 

The second formulation makes clear that the change in behavior results from the mark-to-market loss the investor experiences when the new payout is offered. This is a natural way to think in finance, less natural to a gambler. In this interpretation, the infinite series of doubling payouts does not ruin the Kelly bettor by enticing him to overbet, it extracts all his wealth through changes beyond his control.

 

두 번째 해석은 새로운 배당이 제시될 때 투자자가 경험하는 시장가치 손실로 인해 행동 변화가 발생한다는 점을 명확히 보여줍니다. 이는 금융에서 자연스러운 사고 방식이지만, 도박사에게는 덜 자연스럽습니다. 이 해석에서는 배당이 두 배씩 늘어나는 무한 시리즈가 켈리 베팅자를 과도하게 베팅하게 만들어 파산시키는 것이 아니라, 통제할 수 없는 변화를 통해 그의 재산을 모두 빼앗는 것으로 나타납니다.

 

추가설명 : 위에 해결책 따로 보지 않아도 됩니다. 위에서 왜 역설적인지 설명을 했는데, 조금 더 쉽게 설명 하자면 '도박을 한 번 했는 데 갑자기 조건이 좋아지거나 나빠지면, 처음 계획대로 해야할까? 다르게 해야할까? 라는 것의 문제입니다.

 

켈리공식은 다시 말하면 '하나의 사건(독립적인 사건)'에 대해서 최적의 베팅비율을 계산하는 공식입니다.

 

따라서 이건 '역설이 아니다'라는 관점에서는, 원래 기대값들을 다 예상 한 상태로 베팅비율을 최적화 한 것인데 그 조건이 바뀌게 되면 '그 이전에 베팅'한 것은 잘못 베팅했을 수 있다는 것이니까요.

 

조건부 결과값이 바뀌게 되면 결과 값이 바뀌게 됩니다. 이를테면 첫 도박에 많이 걸었으면, 두번째 기회에 걸 돈이 부족해집니다. 이 경우, 결국 처음부터 5배 배당이 주어졌을 때 보다 손해를 보게 되는 것과 다름이 없습니다. 만약 반대로 2번째 내기에서 배당조건이 처음보다 더 나빠지면, 첫 도박에 걸었던 돈을 더 줄였어야 하는 겁니다.

 

켈리기준이 문제없이 작동하려면 배당률이나 확률이 변하지 않아야합니다. '변동성'이 베팅비율을 높여버린 셈이라고 생각될 수 있습니다. 상황이 바뀌고 배당률이 달라지면, 이 변동성이 결과적으로 베팅비율을 높이는 역할을 한 것이죠.

 

현실에서는 조건은 얼마든지 변할 수 있죠. 왜냐면? 가격과 가치가 존재하기 때문에 '가격'이 떨어진 곳에 그제서야 베팅을 하게 된다면 '예상 상승결과값'이 그 이전에 베팅했었을 때랑 비교하면 기대값 높기 때문에 조건이 달라지기 때문입니다.

 

저도 처음에는 두개의 사건 vs 하나의 사건에 대해서 비교하는 것이 혼란스러웠습니다.

1개의 사건(처음부터 5:1):

• 이 경우, 도박자는 처음부터 5:1 배당금을 알고 있으며, 이에 따라 Kelly 공식을 사용해 재산의 40%를 베팅합니다.
• 이 상황에서 도박자는 단일 사건에 대해 Kelly 공식을 적용한 것입니다.

2개의 사건(2:1 -> 5:1):

• 이 경우, 도박자는 첫 번째로 2:1 배당금을 받았을 때 Kelly 공식을 사용해 재산의 25%를 베팅합니다.
• 이후 두 번째로 5:1 배당금을 받게 되면, 두 번째 Kelly 공식에 따라 추가적으로 재산의 22.5%를 베팅합니다.
• 여기서 중요한 점은 두 번의 연속적인 베팅 사건이 일어났다는 것입니다. 각 사건이 독립적으로 Kelly 공식에 따라 최적화된 베팅 비율을 계산했습니다.

이 두 사건을 비교하려는 것은 구조적으로 다릅니다. 왜냐하면 두 사건은 각기 다른 베팅 기회(다른 사건 수)를 가졌기 때문입니다.

 

왜 이 비교가 말이 안 될 수 있는가?

• 1개의 사건과 2개의 사건은 동일한 맥락에서 비교될 수 없습니다. 두 개의 사건을 한 사건으로 합친다고 해도, 결과적으로는 Kelly 공식이 각 사건을 개별적으로 계산한 것이기 때문입니다.
• 연속적인 베팅에서 Kelly 공식은 각각의 베팅에서 최적화된 베팅 비율을 제공하는데, 이는 각 사건을 독립적으로 최적화합니다. 즉, 첫 번째 사건에서 25%를 베팅한 후 두 번째 사건에서 22.5%를 추가로 베팅하는 구조는 자연스럽게 총합 47.5%의 베팅을 하게 됩니다.
• 반면에, 처음부터 5:1 배당금이 주어졌다면, 도박자는 한 번의 기회에서 재산의 40%를 베팅하는 것이 최적입니다. 이 상황에서는 단 한 번의 베팅만 하므로 추가 베팅이 없습니다.

비교가 가능한 방법

비교를 하려면 동일한 조건을 설정해야 합니다. 예를 들어:

• 연속적인 두 베팅(2:1에서 5:1으로 가는 경우) vs 연속적인 두 베팅이지만 처음부터 5:1인 경우를 비교할 수 있습니다.
• 즉, 두 번째 상황에서도 첫 번째 베팅과 두 번째 베팅을 각각 동일하게 비교하는 방식입니다.

만약 처음부터 5:1의 조건이 주어졌다면, 두 번에 나누어 베팅하는 대신 한 번에 40%를 베팅하므로, 총 베팅 금액은 다릅니다. 이 비교가 혼란스러운 이유는 두 사건과 하나의 사건을 동일선상에서 비교하려 했기 때문입니다. 이를 분리하여 이해하면 더 명확하게 보일 것입니다. 즉,  하나의 베팅 사건과 연속적인 두 개의 베팅 사건을 비교하는 것은 서로 다른 상황입니다.

 

kelly 공식은 각 베팅에서 장기적인 성장률을 최대화 하는 비율을 계산하지만, 연속적인 베팅에서 각기 다른 비율이 누적될 수 있습니다. 때문에 각 베팅은 독립적이지만, 도박자는 계속해서 재산의 일부를 잃을 가능성이 존재합니다. 특히 두번 연속 잃게 된다면, 첫번째 베팅에서 25%를 잃고, 두번째 베팅에서 또 추가로 22.5%를 잃게 되어, 총 재산의 47.5%를 잃게 됩니다. 이 경우에 급격하게 재산이 줄어들어 다음 베팅에서 회복이 어려워집니다.(이 말이 이해가 잘 안간다면? 직관적으로 시각화를 해서 보는 것이 편한데요.)

 

https://blog.naver.com/gambari90/222314878796

[켈리공식 A to Z] 0-4. 운이 높다 vs 운이 낮다?

저는 그것을 운이 '높은'영역과 '낮은' 영역으로도 표현을 하였습니다. 확률적 우위가 있을 떄 적게 베팅할수록 무한한 미래의 가능성에서 장기적으로 기하수익률이 0보다 클 확률이 높은 영역이 더 넓게 나오는 것입니다. kelly 공식이 기하수익률을 최대화하는 것은 맞지만, 미래의 여러가능성 중에서는 운이 '높은'영역을 줄여버리기도 하니까요. 이 부분을 '우산을 든 투자자'에서 잘 설명하고 있습니다.

 

https://blog.naver.com/82doublez/223192573578

산술평균과 기하평균 : 평균 수익률의 함정 (켈리비)

저보다 더 잘 설명한 블로거분의 포스팅 링크를 걸어둡니다.

 

결론적으로, 독립적인 사건을 연속적해서 꾸준히 베팅하다가 보면, 자금이 0에 가까이 오게되는 상황이 올 수 있다는 내용입니다. 기하수익률만을 높이는 kelly criterion은 기하수익률 최대화에만 초점을 맞춘 나머지, 내가 맞이할 미래에서 안좋은 빈도를 맞게할 수 있다는 결론을 내리게 합니다.

 

'확률과 결과값 그리고 기대값'은 '불확실성'을 다루기 때문에, 혼돈스러운 것이 사실입니다. 모건하우절의 <불변의 법칙>에서는 이를 이렇게 표현하기도 합니다.

누군가가 어떤 일이 일어날 거라 말했는데 실제로 일어나면, 그 사람의 예측이 옳은 것이다. 누군가가 어떤일이 일어날 거라고 말했는데 일어나지 않으면, 그 사람의 예측이 틀린 것이다. 사람들은 이런식으로만 생각한다. 그렇게 생각하는 것이 정신적 에너지가 덜 들어가고 편하기 때문이다. 눈앞에 실제 결과가 나와 있는 상태에서 어쩌면 다른 결과가 나올 수도 잇었다는 사실을 사람들에게(또는 자기 자신에게) 납득시키기는 어렵다.